Value at Risk Calculation on High Ingestion Data for Real-Time Trading
Practitioners in the financial industry are commonly confronted with the task of estimating the risks of their positions. Specifically, risk estimation allows them to measure and control their risk exposure when planning their investment and trading strategies. Value at Risk (VAR) is a rather simple yet valuable risk estimation measure, which helps traders and investors understand the risk of loss for their investments. Using VaR financial professionals can estimate how much their investments could lose in a specified time window (e.g., during a day or month) under normal market conditions.
VaR can be calculated at different levels and granularities. For example, it can used to estimate the risk of a single asset or of a portfolio of assets. This is a very common use of VaR by commercial banks and investment organizations, which wish to estimate and understand the potential losses of their institutional portfolios. Nevertheless, VaR is sometimes used firm-wide i.e. to determine the cumulative risk stemming from multiple positions that are typically held by different departments. The latter can be very useful for large investment firms and trading organizations.
From a statistical perspective VaR quantifies the maximum potential losses over a specified timeframe with a degree of confidence. Confidence is therefore an important parameter of VaR calculation. For example, if for a given portfolio the 95% confidence of a one-day VAR is 100.000 EUR, this means that there is a 95% confidence that the portfolio will not lose more than 100.000 EUR within a day. 95% and 99% are the most common confidence internals used in VaR calculation.
Value at Risk Calculation Methods
Many VaR calculation methods have been proposed in the financial engineering and digital finance literature. Three of the most popular ones are:
- The Historical Method: This is probably the simplest VaR calculation method. It relies on significant volumes of historical market data (e.g., typically one trading year data for conventional assets and much more than that for hedge funds) to calculate the price changes for all the assets of the portfolio. Accordingly, it calculates the value of the portfolio for each one of the price changes i.e. the value of the portfolio is simulated many times in-line with the number of price changes in the historic data (e.g., approx. 250-260 times for one trading year). These simulated/estimated values for the portfolio can be sorted and used to form a distribution. Then the VaR at a given confidence level (e.g., 99%) is computed as the mean of the simulated values minus the lowest values (e.g., 1% lowest value for the 99% case) in the series of simulated portfolio values.
- The Variance-Covariance Method :This is also called parametric method. It assumes that returns follow a normal distribution, which is a simplistic yet acceptable assumption during normal market conditions. Given this assumption two parameters can be computed i.e. an expected return and a standard deviation for the portfolio. In case of a portfolio with many assets, the standard deviation should consider the correlation in the price changes of the different assets. The latter requires the computation of the covariance matrix of the various assets (i.e. the correlation co-efficient of the assets). Based on the mean and the variance of the portfolio its value distribution is calculated and the value at the 95% or 99% confidence internal is produced. The method works quite well when there a large sample size for the assets of the portfolio, as well as when the distributions of the asset prices are known.
- The Monte Carlo Method: This method develops randomly scenarios for the future price of the portfolio based on some non-linear pricing models. Accordingly, it creates the distribution of these future prices and takes their losses at the target confidence internal. The method is more reliable when dealing with complex portfolios and complicated risk factors. Its basic assumption is that risk factor has a known probability distribution i.e. that market factors follow certain stochastic processes which are used to estimate future prices.
Real-Time and High Ingestion Challenges
From a financial and statistical perspective there are some known limitations of VaR calculation. First, the calculations are based on some assumptions, which are used to formulate the inputs to the various calculation methods. In cases where these assumptions are not valid, the Var outcome cannot be reliable. For instance, VaR methods are not effective in cases of bear markets such as during the financial crises of 2001 and 2008. Likewise, different methods can lead to different VaR outcomes for the same portfolios. Moreover, as evident from the methods outlined above, calculations become more challenging for larger portfolios, where the correlations between many assets need to be accounted for.
Despite these limitations, the implementation of VaR from a technical perspective is quite straightforward given the statistical computing tools (e.g., scientific computing libraries) that are nowadays available. However, the technical part of VaR solutions can become more challenging in real-time trading scenarios, where there is a need for dealing with large volumes of data that feature very high ingestion. In such cases, conventional databases and data management tools are pushed at their limits and BigData techniques must be applied.
The INFINITECH VaR Pilot
This is the case with VaR calculation experiments in the scope of the H2020 INFINITECH project, Europe’s flagship project for Artificial Intelligence (AI) and BigData in Digital Finance. In INFINITECH, INNOV-ACTS is contributing to the development a real-time VaR calculation system for Forex (FX) trading portfolios. Our objective is to offer live insights on FX VaR to enable traders perform real-time time what-if analysis in their positions.
The initial MVP of the solution calculate the VaR-95% and VaR-99% values for different FX portfolios, using all the three presented methods, as illustrated in the following diagram. The system is interfacing to the low-level streaming capabilities of the LeanXcale database towards reading and processing data with very high ingestion rates.
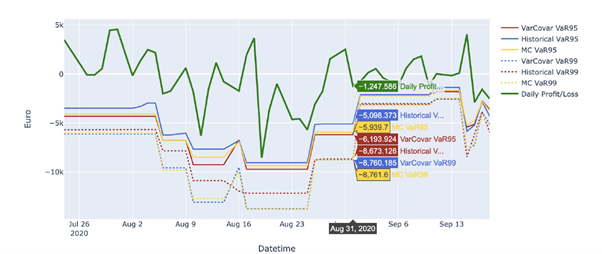
Our development roadmap includes validation and benchmarking of the systems with large volumes of data and a mass of calculations, as well as the employment of machine learning techniques in conjunctions with our Monte Carlo simulations. Stay tuned!
Follow as on Twitter: @Infinitech_EU for updates on the INFINITECH-RA and use cases!
